Teorema:
Sea T el sistema de axiomas para la teoría de conjuntos obtenido de
sistema de V. Neumann S* al omitir el axioma de elección luego,
si T es consistente, lo sigue siendo, si las siguientes proposiciones 1-4 se unen simultáneamente como nuevos axiomas:
1. El axioma de la elección
2. La hipótesis del continuo generalizado (es decir, la afirmación de que 2^א= א_(α+1) es válido para cualquier ordinal α)
3. La existencia de conjuntos lineales no medibles tales que tanto ellos como sus complementos son proyecciones uno a uno de complementos bidimensionales de conjuntos analíticos
4. La existencia de complementos lineales de conjuntos analíticos, que son de el poder del continuo y no contienen ningún subconjunto perfecto.
Un teorema correspondiente también válido si T denota el sistema de axiomas de Fraenkel para la teoría de conjuntos, dejando fuera el axioma de elección pero incluyendo el axioma de infinito.
La demostración de los teoremas anteriores es constructiva en el sentido de que, si se obtuviera una contradicción en el sistema ampliado, se podría mostrar una contradicción en T.
El método de prueba consiste en construir sobre la base de los axiomas de T un modelo para el cual las proposiciones 1-4 son verdaderas (Esto significa que el modelo se construye mediante métodos esencialmente transfinitos y, por lo tanto, proporciona solo una prueba relativa de consistencia, lo que requiere la consistencia de T como hipótesis).
Este modelo, en términos generales, consta de todos los conjuntos "matemáticamente construibles", esto significa que los conjuntos "construibles" se definen como aquellos conjuntos que pueden obtenerse mediante la jerarquía de tipos ramificada de Russell, si se amplían para incluir órdenes transfinitos.
La extensión a órdenes transfinitos tiene la consecuencia de que el modelo satisface los axiomas impredicativos de la teoría de conjuntos, porque se puede probar un axioma de reducibilidad para órdenes suficientemente altos.
Además, se puede probar que la proposición "Todo conjunto es construible" (que abreviaremos con A) es consistente con los axiomas de T, porque A resulta ser verdadera para el modelo que consta de los conjuntos construibles.
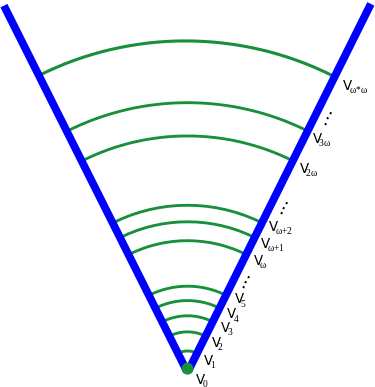
De A se pueden deducir las proposiciones 1-4. En particular, la proposición 2 se sigue del hecho de que todos los conjuntos construibles de enteros ya se obtienen para órdenes <ω, todos los conjuntos construibles de conjuntos de enteros para órdenes <ω_2 y así sucesivamente.
La proposición A agregada como un nuevo axioma parece dar una terminación natural de los axiomas de la teoría de conjuntos, en la medida en que determina la vaga noción de un conjunto infinito arbitrario de una manera definida.
En esta conexión es importante que la prueba de consistencia para A no se rompa si se unen axiomas de infinito más fuertes (por ejemplo, la existencia de números inaccesibles) a T.
Por tanto, la consistencia de A parece ser absoluta en algún sentido, aunque no es posible en el estado actual de las cosas dar un significado preciso a esta frase.
Referencias:
Hrbacek, K. and Jech, T., 1978. Introduction To Set Theory
Jech, T., 1997 Set Theory
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1077160/pdf/pnas01800-0034.pdf
Σχόλια