El Universo Constructible de Gödel
- Edison Huérfano

- 18 nov 2020
- 2 Min. de lectura
Actualizado: 13 dic 2020
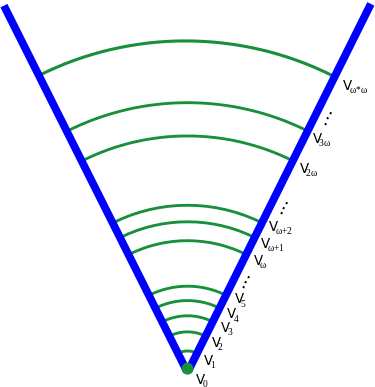
El universo de constructible de Gödel, o solamente el universo constructible, se denota L y es la unión de la jerarquía L alpha. En esta jerarquía se construyen las étapas de manera similar al universo de von Neumann, visto en clase. Cada étapa tiene un ordinal correspondiente y el universo L es definido por recursión transifinita en ordinales, en pasos de du sucesor. No se toma el conjunto potencia, como con von Neumann se toma Vα para obtener V{α+1} , sino que sólo se toma los subconjuntos de Lα que son definibles en Lα , usando elementos de Lα para esto.
Veamos
Definición. Sea P[Def] el conjunto de todos los subconjuntos de X que son definibles en la estructura (X, ∈) por una formula del lenguaje de la teoría de conjuntos ϕ, usando elementos de X como parámetros de la definición. Sean, además,
Entonces L la unión de todos los Lα, para α ordinal. Esto es,
donde Ord es la clase de todos los ordinales.
Ahora veamos, si
entonces x es definible en la estructura (Lα, ∈) porque sus elementos y ∈ x están también en Lα. Esto es,
Es decir, que Lα es un subconjunto de L{α+1}, y este a su vez es un subconjunto de Lα. Es por esto que podemos decir que la clase L es una jerarquía de conjuntos transitivos anidados. Además, L es constructible. Se dice que ⟨ Lα : α ∈ Ord ⟩ es una jeraquía acumulativa
Los elementos de L se denominan conjuntos construibles y L en sí mismo es el universo construible.
Referencias
[1] Bagaria, Joan, "Set Theory", The Stanford Encyclopedia of Philosophy (Spring 2019 Edition), Joan Bagaria (ed.), URL = https://plato.stanford.edu/archives/entries/set-theory/
[2] Jech, T. (2002). Set Theory (3rd ed.). Springer.



Comentarios